Exploring .NET Core platform intrinsics: Part 2 - Accelerating AES encryption on ARMv8
Previous posts in the series:
This is part 2 in a series of posts on using .NET Core platform intrinsics. Part 1 discussed the implementation of SHA-256 using specialized instructions available in the ARMv8 Cryptography Extensions. Part 2 will describe the accelerated implementation of AES encryption using hardware instructions that are part of the same instruction set.
AES is probably the most widely used symmetric encryption algorithm today. It’s a block cipher that can encrypt 128-bit blocks of data using the secret key that can be 128, 196, or 256 bits long. In practice we almost always want to encrypt variable-length messages, which is why block ciphers are inseparable from modes of operation such as CBC, CTR, or GCM. In this post I will talk about AES-128 only as a block cipher, without implementing any particular mode of operation (don’t worry, GCM will be the topic of one of the future posts in this series).
AES block cipher
The only thing you should know about AES in most situations is that it’s pseudo-random permutation that takes a 128-bit input, a 128-bit key, and produces a 128-bit encrypted output. On the other hand, if you want to implement it using specialized hardware instructions, you have to know just a little bit more about how the AES black box works internally.
AES is defined in the NIST’s FIPS 197 publication, but we are currently interested only in high-level description of the algorithm, which can be found on Wikipedia (some people also like the Stick Figure Guide to the Advanced Encryption Standard). For those who dislike clicking the links in the middle of a blog post, here’s the pseudocode of the encryption algorithm:
var rounds = 10;
var state = input;
AddRoundKey(state, roundKeys[0]);
for (int i = 1; i < rounds; ++i)
{
SubBytes(state);
ShiftRows(state);
MixColumns(state);
AddRoundKey(state, roundKeys[i]);
}
SubBytes(state);
ShiftRows(state);
AddRoundKey(state, roundKeys[rounds]);
You can see that the core of the algorithm is actually pretty simple (the individual operations are more complicated, but at this moment we don’t care about what they are doing internally). We have 11 different round keys generated from the main key, and four basic operations performed over 10 rounds. First 9 rounds are the same; the last one is slightly different as it does not include the MixColumns step.
Decryption works in a similar fashion. Each transformation has its inverse, so all the decryption algorithm has to do is to perform the inverse operations in the reverse order. Because encryption and decryption are very similar to each other, I’ll only talk about the encryption in the remainder of this post to avoid repeating myself (the decryption function will be available in the GitHub repository accompanying this post).
ARMv8 AES intrinsics
Now that you are familiar with the basic algorithm, let’s see which hardware instructions are available to us:
- AESE (AES single round encryption)
- AESD (AES single round decryption)
- AESMC (AES mix columns)
- AESIMC (AES inverse mix columns)
Looks like almost everything we need is here. AESE combines the AddRoundKey, SubBytes, and ShiftRows steps, and AESMC performs the MixColumns step, believe it or not! The only thing that is missing is the instruction for generating the round keys (Intel has the AESKEYGENASSIST instruction for that purpose), which I will talk about later.
If you were following closely, you might have noticed that because the instructions don’t map one-to-one to AES rounds, we don’t have the last AddRoundKey operation covered. AddRoundKey is just a plain old bitwise XOR operation, which is why we can implement it with the simple VEOR instruction. All of this is best shown in this gorgeous diagram that I personally created:
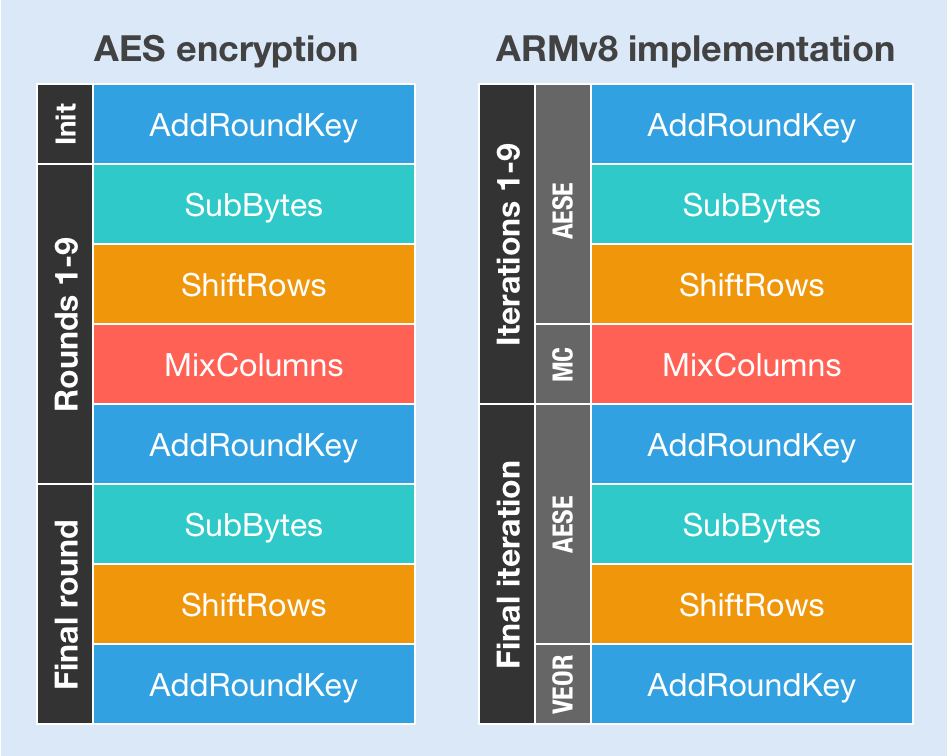
As I mentioned previously, we are not much interested in the instructions themselves. What we care about are the C language intrinsics for using them, and they are defined like this:
// Performs AES single round encryption
uint8x16_t vaeseq_u8(uint8x16_t data, uint8x16_t key);
// Performs AES single round decryption
uint8x16_t vaesdq_u8(uint8x16_t data, uint8x16_t key);
// Performs AES mix columns
uint8x16_t vaesmcq_u8(uint8x16_t data);
// Performs AES inverse mix columns
uint8x16_t vaesimcq_u8(uint8x16_t data);
The C# API looks pretty much the same:
public static class Aes
{
public static bool IsSupported { get; }
public static Vector128<byte> Decrypt(Vector128<byte> value, Vector128<byte> roundKey);
public static Vector128<byte> Encrypt(Vector128<byte> value, Vector128<byte> roundKey);
public static Vector128<byte> MixColumns(Vector128<byte> value);
public static Vector128<byte> InverseMixColumns(Vector128<byte> value);
}
C# implementation
The first thing we need to do is to expand the secret key into 11 round keys. We don’t have the intrinsics that can help us with that, so we have to implement the key expansion from scratch. The key expansion is not particularly interesting, so I will not talk about it here—I will just use the pre-expanded round keys instead. If you ever need to implement it in C#, the easiest way to do so would be to just copy the definition of GenerateKeyExpansion function from the RijndaelManagedTransform class, which is a part of the .NET Framework standard library.
The code implementing the encryption is relatively short and very easy to follow, so I’ll just show you the entire Encrypt function here:
public void Encrypt(byte[] input, byte[] output)
{
int position = 0;
int left = input.Length;
var key0 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[0 * BlockSize]);
var key1 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[1 * BlockSize]);
var key2 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[2 * BlockSize]);
var key3 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[3 * BlockSize]);
var key4 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[4 * BlockSize]);
var key5 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[5 * BlockSize]);
var key6 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[6 * BlockSize]);
var key7 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[7 * BlockSize]);
var key8 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[8 * BlockSize]);
var key9 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[9 * BlockSize]);
var key10 = Unsafe.ReadUnaligned<Vector128<byte>>(ref enc[10 * BlockSize]);
while (left >= BlockSize)
{
var block = Unsafe.ReadUnaligned<Vector128<byte>>(ref input[position]);
block = Aes.Encrypt(block, key0);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key1);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key2);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key3);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key4);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key5);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key6);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key7);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key8);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key9);
block = Simd.Xor(block, key10);
Unsafe.WriteUnaligned(ref output[position], block);
position += BlockSize;
left -= BlockSize;
}
}
Everything looks pretty ordinary here. We are using the fact that we have plenty of registers available to load all the round keys prior to the actual encryption, so we can process multiple blocks of data much faster, in a single invocation of the function. Each round is just one Encrypt/MixColumn combo, except the last one, which replaces the MixColumns step with the AddRoundKey (implemented with the simple call to Xor function from the Simd class in the Arm64 namespace). Now let’s see how fast we are going!
Performance
The setup for measuring performance was the same as the one from the previous post: Scaleway cloud instance for running the code, BenchmarkDotNet for running the benchmarks, AES implementation from the .NET standard library (which is again using OpenSSL behind the scenes), and BouncyCastle’s managed implementation. This time, though, two different AES classes were available in BouncyCastle: one was slow and safe, and the other one was fast, but not resistant to cache-timing attacks (side-channel attack resistance is one of the main reasons for the existence of AES hardware instructions, because safely implementing AES by hand is incredibly tricky). Without further ado, here are the numbers:
| Method | Mean | Error | StdDev |
|---|---|---|---|
| OpenSsl16B | 845.92 ns | 0.3094 ns | 0.2894 ns |
| Intrinsics16B | 69.18 ns | 0.0064 ns | 0.0060 ns |
| BouncyCastleSlow16B | 1,236.72 ns | 0.2859 ns | 0.2534 ns |
| BouncyCastleFast16B | 1,130.88 ns | 0.3798 ns | 0.3552 ns |
| OpenSsl1K | 3,970.90 ns | 0.2851 ns | 0.2527 ns |
| Intrinsics1K | 2,560.72 ns | 0.2241 ns | 0.2097 ns |
| BouncyCastleSlow1K | 67,591.19 ns | 4.9099 ns | 4.5927 ns |
| BouncyCastleFast1K | 59,282.02 ns | 2.9021 ns | 2.7146 ns |
| OpenSsl1M | 3,521,992.27 ns | 165.1864 ns | 154.5154 ns |
| Intrinsics1M | 2,899,086.42 ns | 176.2553 ns | 164.8693 ns |
| BouncyCastleSlow1M | 69,124,217.92 ns | 2,713.7717 ns | 2,538.4635 ns |
| BouncyCastleFast1M | 60,573,568.95 ns | 2,857.6861 ns | 2,673.0811 ns |
The results are much more impressive this time. BouncyCastle is orders of magnitude slower, as expected. But the intrinsics implementation is also noticeably better than OpenSSL in each category of inputs: 16B, 1K, and 1M.
Single block comparison may look slightly unfair, though, as it includes big overhead of several function calls and whatnot. Nevertheless, it’s very important when implementing some non-standard modes of operation which use AES block cipher as a basic building block—if we can’t encrypt a single block efficiently, the performance of the whole construction suffers greatly.
Now that the victory is officially declared, are we done here? Not just yet—we can do even better!
Pipelining
Modern processors are complex beasts that can juggle multiple instructions at the same time. Thanks to pipelining, we can have several instructions that take multiple cycles to execute running at the same time, each of them being in the different phase of its execution. How can we take advantage of that in our case? Let’s go back to this snippet of code from our encryption function:
var block = Unsafe.ReadUnaligned<Vector128<byte>>(ref input[position]);
block = Aes.Encrypt(block, key0);
block = Aes.MixColumns(block);
block = Aes.Encrypt(block, key1);
block = Aes.MixColumns(block);
Each Encrypt/MixColumns function call depends on the output of the previous operation, which means the instructions cannot be executed in parallel. We can, however, process multiple input blocks at the same time! For example, if we want to handle four blocks in one loop iteration, we can rearrange the code to look like this:
var block0 = Unsafe.ReadUnaligned<Vector128<byte>>(ref input[position + 0 * BlockSize]);
var block1 = Unsafe.ReadUnaligned<Vector128<byte>>(ref input[position + 1 * BlockSize]);
var block2 = Unsafe.ReadUnaligned<Vector128<byte>>(ref input[position + 2 * BlockSize]);
var block3 = Unsafe.ReadUnaligned<Vector128<byte>>(ref input[position + 3 * BlockSize]);
// Round 1
block0 = Aes.Encrypt(block0, key0);
block1 = Aes.Encrypt(block1, key0);
block2 = Aes.Encrypt(block2, key0);
block3 = Aes.Encrypt(block3, key0);
block0 = Aes.MixColumns(block0);
block1 = Aes.MixColumns(block1);
block2 = Aes.MixColumns(block2);
block3 = Aes.MixColumns(block3);
We are now issuing four independent AESE/AESMC instructions sequentially, which should be much more efficient from the pipelining perspective. The numbers are confirming that hypothesis:
| Method | Mean | Error | StdDev |
|---|---|---|---|
| Intrinsics1K | 2,560.72 ns | 0.2241 ns | 0.2097 ns |
| IntrinsicsPipelined1K | 1,919.83 ns | 0.1546 ns | 0.1447 ns |
| Intrinsics1M | 2,899,086.42 ns | 176.2553 ns | 164.8693 ns |
| IntrinsicsPipelined1M | 2,094,697.83 ns | 149.5739 ns | 139.9115 ns |
The performance boost is clearly visible (although not as much as I have expected). This trick is not always applicable, though. Remember that we always have to combine some mode of operation with the actual block cipher? Well, not all modes can take advantage of encrypting multiple blocks at the same time. However, some modes of operation such as CTR and GCM are inherently parallelizable, which is where this optimization really shines.
How did I come up with the number four for the number of instructions issued at the same time? Performance of each instruction is defined by its latency (number of cycles needed to complete the instruction) and throughput (number of cycles before another instruction of the same type can be issued). You can read the Cortex-A57 Software Optimization Guide to get the rough idea how some instruction will perform on the ARMv8 platform, but ultimately you have to measure and see what works best for you in practice.
Conclusion
You can find the complete C# implementation of both AES encryption and decryption in my ARMv8 AES intrinsics GitHub repository (it currently serves only as a demo, not as a production-ready implementation). In the next post we will take a break from writing the code and explore the various ways to see the instructions emitted by the JIT.