Exploring .NET Core platform intrinsics: Part 4 - Alignment and pipelining
Previous posts in the series:
- Exploring .NET Core platform intrinsics: Part 1 - Accelerating SHA-256 on ARMv8
- Exploring .NET Core platform intrinsics: Part 2 - Accelerating AES encryption on ARMv8
- Exploring .NET Core platform intrinsics: Part 3 - Viewing the code generated by the JIT
You’ve implemented some of your performance critical code using the new platform intrinsics API. The code is now running 10x or even 100x faster than before, and you might think that it can’t get any faster. This post will show you some less obvious (but almost universally applicable) techniques for improving the performance even further.
The code
This time we are going to analyze the function that calculates the sum of an array of integers:
public static int Sum(int[] source)
{
const int VectorSizeInInts = 8;
fixed (int* ptr = &source[0])
{
var pos = 0;
var sum = Avx.SetZeroVector256<int>();
for (; pos <= source.Length - VectorSizeInInts; pos += VectorSizeInInts)
{
var current = Avx.LoadVector256(ptr + pos);
sum = Avx2.Add(current, sum);
}
var temp = stackalloc int[VectorSizeInInts];
Avx.Store(temp, sum);
var final = Sum(temp, VectorSizeInInts);
final += Sum(ptr + pos, source.Length - pos);
return final;
}
}
Nothing fancy here—it just follows the pattern that we see very often when dealing with vectorized code. Let’s see how well it performs.
Benchmarking, take one
We will measure how long it takes to sum an array of 32K integers. Our benchmarking setup is going to be very simple:
public class SumBenchmark
{
private const int Length = 32 * 1024;
private int[] data;
[GlobalSetup]
public void GlobalSetup()
{
data = Enumerable.Range(0, Length).ToArray();
}
[Benchmark]
public int Sum() => FastMath.Sum(data);
}
This benchmark produces the following numbers on my machine:
| Method | Mean | Error | StdDev |
|---|---|---|---|
| Sum | 2.264 us | 0.0352 us | 0.0329 us |
The results look fantastic, beating the naive implementation by one order of magnitude (if you are interested in the exact numbers, take a look here).
You want to be sure that there are no variations, so you run the benchmark several times to increase your confidence in the results, but you get pretty much the same numbers on each run. Is it time to call it a day? Not just yet: even though the SumBenchmark class looks completely reasonable, it contains one very subtle flaw.
Benchmarking, take two
Let’s modify our benchmarking code slightly:
[GlobalSetup]
public void GlobalSetup()
{
data1 = Enumerable.Range(0, Length).ToArray();
data2 = Enumerable.Range(0, Length).ToArray();
}
[Benchmark(Baseline = true)]
public int Sum1() => FastMath.Sum(data1);
[Benchmark]
public int Sum2() => FastMath.Sum(data2);
You would probably expect both Sum1 and Sum2 to have the identical performance characteristics. After all, we are calling the same function on two arrays with the exact same contents. But if you run the benchmark, you will see that Sum2 actually performs 13% worse!
| Method | Mean | Error | StdDev | Scaled |
|---|---|---|---|---|
| Sum1 | 2.283 us | 0.0211 us | 0.0198 us | 1.00 |
| Sum2 | 2.589 us | 0.0241 us | 0.0214 us | 1.13 |
What is going on here?
Alignment
When working with most of AVX instructions, you initially have to load the data from the memory into 32-byte registers. The CPU does that in the most efficient way when the data is aligned in memory on a 32-byte boundary. How does that apply to our situation?
In one of the runs of the modified benchmark, the data1 array was located at the address 0x19aa99ce0, while the data2 was placed at 0x19aab9d18. The first number is divisible by 32; the second one is not. That was not just a coincidence: each time I ran the benchmark, the first allocation ended up on a properly aligned address, but the second one didn’t (I guess that the heap segments are aligned, which would mean that the first allocated object in the program would also be aligned, but I didn’t bother to check that hypothesis, so it might be terribly wrong).
Dealing with an alignment is burdensome, which is why the LoadVector256 function works with any memory location—it just works slower when the location is unaligned. There is also another variant of Load function, called LoadAlignedVector256, which works the same in the aligned case (it’s not any faster), but throws an exception if the input is not aligned on a 32-byte boundary. It’s useful mostly as a signal that its input is expected to be aligned.
There are no guarantees that our input array is always going to be correctly aligned, so you might think that we can’t do anything about the performance in the unaligned case. Luckily, we don’t have to start processing the array from the first element—instead we can find the first aligned element, and proceed from there (that means we have to calculate the sum of previous elements manually). To do that, we just have to round up the address of our array to the nearest multiple of 32:
var aligned = (int*)(((ulong)ptr + 31UL) & ~31UL);
var pos = (int)(aligned - ptr);
var final = Sum(ptr, pos);
The rest of the code remains the same (we can also replace the call to LoadVector256 with the call to LoadAlignedVector256 in order to catch potential bugs in our code more easily). We can now expect the best-case performance on any input, but we still have to confirm that in practice:
| Method | Alignment | Mean | Error | StdDev | Scaled |
|---|---|---|---|---|---|
| Sum | 8 | 2.508 us | 0.0353 us | 0.0313 us | 1.00 |
| SumAligned | 8 | 2.260 us | 0.0106 us | 0.0082 us | 0.90 |
| Sum | 32 | 2.254 us | 0.0187 us | 0.0166 us | 1.00 |
| SumAligned | 32 | 2.264 us | 0.0256 us | 0.0227 us | 1.00 |
We are indeed getting the expected 10% performance improvement on unaligned arrays! Nothing spectacular, but we are not stopping there.
Pipelining
I’ve already talked briefly about pipelining in the second post of this series, so you might want to take a look at it if you want to refresh your memory. Now let’s see if it’s possible to apply it somehow in our Sum function. Here’s what the documentation for the _mm256_loadu_si256 intrinsic says (the page for the _mm256_load_si256 is almost the same):
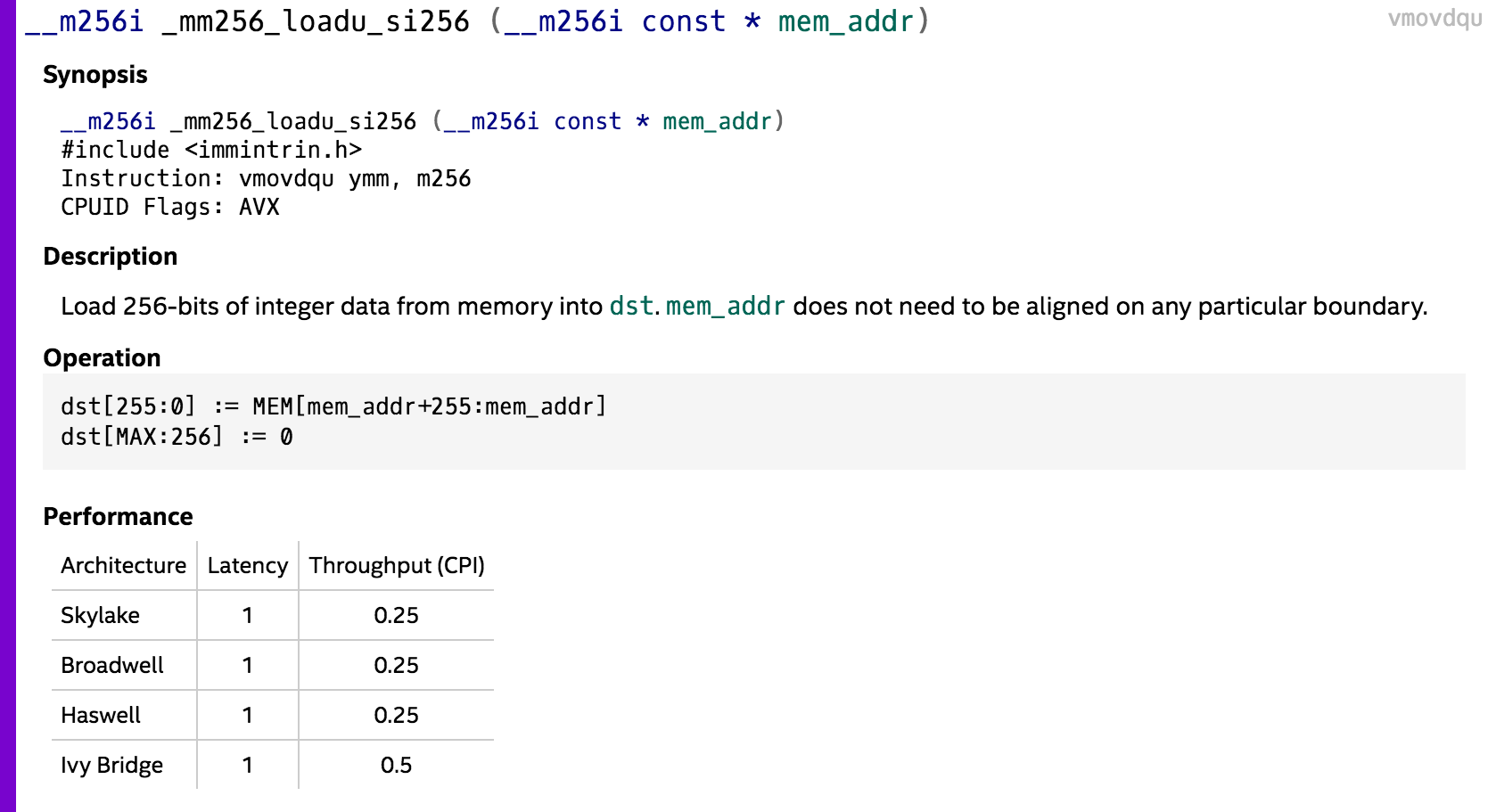
The properties we are interested in are latency and throughput. We can see that the instruction has a latency of 1, which means it takes one CPU cycle to complete. What is more interesting is that it has a throughput of 0.25 (except on Ivy Bridge, where its throughput is 0.5), which is just another way of saying that we can issue four instructions in the same cycle! It means that if we changed our code to process four 32-byte blocks of input at the same time, we could expect at least some performance improvement. Here’s the modified version of the code:
const int VectorSizeInInts = 8;
const int BlockSizeInInts = 32;
for (; pos <= source.Length - BlockSizeInInts; pos += BlockSizeInInts)
{
var block0 = Avx.LoadVector256(ptr + pos + 0 * VectorSizeInInts);
var block1 = Avx.LoadVector256(ptr + pos + 1 * VectorSizeInInts);
var block2 = Avx.LoadVector256(ptr + pos + 2 * VectorSizeInInts);
var block3 = Avx.LoadVector256(ptr + pos + 3 * VectorSizeInInts);
sum = Avx2.Add(block0, sum);
sum = Avx2.Add(block1, sum);
sum = Avx2.Add(block2, sum);
sum = Avx2.Add(block3, sum);
}
for (; pos <= source.Length - VectorSizeInInts; pos += VectorSizeInInts)
{
var current = Avx.LoadVector256(ptr + pos);
sum = Avx2.Add(current, sum);
}
Notice that after the first loop is completed, we might still have several vector-sized blocks of data remaining, so we have to run the original loop to process the rest. We are ready to run the benchmark again:
| Method | Alignment | Mean | Error | StdDev | Scaled |
|---|---|---|---|---|---|
| Sum | 8 | 2.556 us | 0.0144 us | 0.0121 us | 1.00 |
| SumPipelined | 8 | 2.116 us | 0.0189 us | 0.0168 us | 0.83 |
| Sum | 32 | 2.264 us | 0.0127 us | 0.0113 us | 1.00 |
| SumPipelined | 32 | 1.654 us | 0.0133 us | 0.0124 us | 0.73 |
The results are looking great! The next obvious step is to combine both alignment and pipelining in the same function.
Combined solution
Here’s the complete source code of the ultimate version of the Sum function:
public static int SumAlignedPipelined(int[] source)
{
const ulong AlignmentMask = 31UL;
const int VectorSizeInInts = 8;
const int BlockSizeInInts = 32;
fixed (int* ptr = &source[0])
{
var aligned = (int*)(((ulong)ptr + AlignmentMask) & ~AlignmentMask);
var pos = (int)(aligned - ptr);
var sum = Avx.SetZeroVector256<int>();
var final = Sum(ptr, pos);
for (; pos <= source.Length - BlockSizeInInts; pos += BlockSizeInInts)
{
var block0 = Avx.LoadAlignedVector256(ptr + pos + 0 * VectorSizeInInts);
var block1 = Avx.LoadAlignedVector256(ptr + pos + 1 * VectorSizeInInts);
var block2 = Avx.LoadAlignedVector256(ptr + pos + 2 * VectorSizeInInts);
var block3 = Avx.LoadAlignedVector256(ptr + pos + 3 * VectorSizeInInts);
sum = Avx2.Add(block0, sum);
sum = Avx2.Add(block1, sum);
sum = Avx2.Add(block2, sum);
sum = Avx2.Add(block3, sum);
}
for (; pos <= source.Length - VectorSizeInInts; pos += VectorSizeInInts)
{
var current = Avx.LoadAlignedVector256(ptr + pos);
sum = Avx2.Add(current, sum);
}
var temp = stackalloc int[VectorSizeInInts];
Avx.Store(temp, sum);
final += Sum(temp, VectorSizeInInts);
final += Sum(ptr + pos, source.Length - pos);
return final;
}
}
And here are the final results:
| Method | Alignment | Mean | Error | StdDev | Scaled |
|---|---|---|---|---|---|
| Sum | 8 | 2.501 us | 0.0284 us | 0.0251 us | 1.00 |
| SumAligned | 8 | 2.271 us | 0.0257 us | 0.0241 us | 0.91 |
| SumPipelined | 8 | 2.103 us | 0.0276 us | 0.0258 us | 0.84 |
| SumAlignedPipelined | 8 | 1.645 us | 0.0126 us | 0.0118 us | 0.66 |
| Sum | 32 | 2.255 us | 0.0243 us | 0.0227 us | 1.00 |
| SumAligned | 32 | 2.277 us | 0.0288 us | 0.0269 us | 1.01 |
| SumPipelined | 32 | 1.661 us | 0.0219 us | 0.0205 us | 0.74 |
| SumAlignedPipelined | 32 | 1.653 us | 0.0063 us | 0.0056 us | 0.73 |
The SumAlignedPipelined shows a noticeable improvement over the initial Sum: we are getting a 27% boost in performance if the data is 32-byte aligned, and 34% if it’s not.
Conclusion
You’ve seen how some very simple techniques can help you speed up your intrinsics code with almost no effort. The complete C# implementation of these performance exercises can be found in my alignment and pipelining GitHub repository.